Weight initialization plays a critical role in the training of neural networks. Proper setup ensures models converge efficiently and perform well. Without it, issues like vanishing or exploding gradients can arise, hindering progress.
Research by Glorot et al. highlights the importance of maintaining activation variance across layers. This approach helps stabilize training and improves optimization efficiency. Poor initialization, on the other hand, can lead to slow convergence or even divergence.
In deep learning, the choice of initialization method directly impacts model accuracy. Techniques like Xavier and He initialization are widely used to address these challenges. Understanding these concepts is essential for building effective machine learning systems.
By focusing on proper initialization, developers can enhance model performance and avoid common pitfalls. This foundational step sets the stage for successful training and reliable results.
Introduction to Weight and Bias Initialization
The foundation of effective training in deep learning lies in proper setup. Without it, models struggle to learn efficiently, leading to poor performance. Proper configuration ensures stable learning and avoids common issues like vanishing or exploding gradients.
Why Initialization Matters in Neural Networks
Activation functions play a key role in how models learn. When parameters are set incorrectly, the flow of gradients during backpropagation is disrupted. This can cause layers to stop learning or grow uncontrollably.
Maintaining variance across layers is essential. It ensures that signals propagate effectively without losing strength. Techniques like Xavier and He initialization address this by balancing parameter values.
Common Challenges in Initialization
One major issue is vanishing gradients. Small parameter values cause gradients to shrink, halting learning. Conversely, large values lead to exploding gradients, making training unstable.
Zero setup creates symmetric behavior in neurons, preventing them from learning distinct features. This symmetry breaks the model’s ability to differentiate patterns effectively.
| Setup Type | Effect on Gradients | Impact on Training |
|---|---|---|
| Proper | Stable flow | Efficient learning |
| Poor | Vanishing/Exploding | Slow or unstable training |
A case study of a 9-layer network with linear activations shows the importance of proper setup. Without it, exponential growth or decay in signals disrupts learning. Mathematical proofs highlight the need for variance preservation across layers.
The Role of Weights and Biases in Neural Networks
Weights and biases are fundamental components that shape the behavior of neural networks. They determine how inputs are transformed into outputs across different layers. Proper configuration ensures efficient learning and optimal performance.
Understanding Weights and Their Impact
Weights define the importance of specific features in the input data. During forward propagation, they are multiplied by the input values to produce weighted sums. This process is mathematically represented as: ŷ = W[L]W[L-1]…W[1]x.
Random initialization breaks symmetry, allowing neurons to learn distinct features. Without this, all neurons would behave identically, limiting the model’s ability to differentiate patterns. Proper weight setup ensures stable gradient flow during backpropagation.
Understanding Biases and Their Role
Biases shift the activation threshold of neurons, enabling flexibility in learning. They allow the model to fit data even when the weighted sum is zero. Typically, biases are initialized to zero to avoid introducing unnecessary complexity at the start.
During training, biases are updated alongside weights to minimize the loss function. This dynamic adjustment ensures the model adapts effectively to the data. Proper bias initialization is crucial for achieving optimal results.
| Component | Role | Initialization |
|---|---|---|
| Weights | Determine feature importance | Random |
| Biases | Shift activation thresholds | Zero |
How to Initialize Weights and Biases in Neural Networks
Effective model training begins with the right setup of parameters. Proper configuration ensures stable learning and avoids common issues like vanishing or exploding gradients. This section provides a detailed guide to initialization techniques and how to choose the best method for your model.

Step-by-Step Guide to Initialization
Start by selecting an appropriate method based on your activation function. For example, Xavier initialization works well with tanh, while He initialization is ideal for ReLU. Here’s a simple framework:
- Identify the activation function used in your model.
- Choose an initialization method that aligns with it.
- Set parameters using random values from a normal distribution or uniform distribution.
For instance, Xavier initialization uses the formula: W[l] ~ N(0, 1/n[l-1]). This ensures variance is preserved across layers, promoting stable training.
Choosing the Right Initialization Method
Different activation functions require specific initialization techniques. Here’s a comparison to help you decide:
| Activation Function | Recommended Initialization |
|---|---|
| ReLU | He Initialization |
| Tanh | Xavier Initialization |
For deeper networks, consider practical factors like gradient clipping to handle exploding gradients. A case study on MNIST classification accuracy highlights the impact of proper setup on model performance.
For more details on initialization techniques, explore this comprehensive guide. Proper setup ensures your model converges efficiently and delivers reliable results.
Zero Initialization: Pros and Cons
Zero initialization is a method that sets all parameters to zero at the start of training. While simple, this approach often leads to significant challenges in model performance. Understanding its limitations and potential uses is essential for effective training.
Why Zero Initialization Fails
One major issue with zero initialization is the creation of identical gradients across neurons. This symmetry prevents neurons from learning distinct features, as all updates during backpropagation are the same. Mathematical proofs show that this leads to a lack of diversity in learning patterns.
In deeper networks, zero initialization exacerbates problems like vanishing gradients. Without proper variance in parameter values, signals fail to propagate effectively through layers. This results in slow or stalled training, making the method unsuitable for complex models.
When Zero Initialization Might Work
Despite its drawbacks, zero initialization can be effective in specific scenarios. For shallow networks with non-linear activation functions, this method may still yield acceptable results. Empirical studies on 3-layer networks demonstrate its potential in simpler architectures.
Additionally, biases are often safely initialized to zero, as they do not contribute to symmetry issues. Modern frameworks default to this practice, ensuring a balanced start for training. However, for weights, small random values or other techniques are generally preferred.
- Mathematical proof highlights gradient symmetry in zero-initialized networks.
- Exception cases include shallow networks with non-linear activations.
- Empirical results from 3-layer network experiments show limited effectiveness.
- Comparison with small constant initialization reveals better alternatives.
- Modern frameworks default to zero initialization for biases only.
Random Initialization Techniques
Random initialization techniques are essential for breaking symmetry in model training. By setting parameters with random values, neurons can learn distinct features, ensuring effective learning. Two common methods are Random Normal and Random Uniform initialization.

These methods differ in their statistical properties. Random Normal uses a normal distribution, while Random Uniform relies on a uniform distribution. Both aim to control variance to ensure stable training.
Random Normal Initialization
Random Normal initialization draws values from a normal distribution with a specified mean and standard deviation. This method is effective for maintaining variance across layers, promoting stable gradient flow.
In TensorFlow, this can be implemented as:
initializer = tf.keras.initializers.RandomNormal(mean=0., stddev=1.)
Adjusting the stddev parameter allows for precise control over the distribution’s spread, reducing the risk of overfitting.
Random Uniform Initialization
Random Uniform initialization samples values from a uniform distribution within a defined range. This method is simpler but equally effective for breaking symmetry in early training stages.
In TensorFlow, it can be implemented as:
initializer = tf.keras.initializers.RandomUniform(minval=0., maxval=1.)
Parameters like minval and maxval ensure values stay within a reasonable range, preventing exploding gradients.
| Initialization Method | Distribution Type | Key Parameters |
|---|---|---|
| Random Normal | Normal | Mean, Stddev |
| Random Uniform | Uniform | Minval, Maxval |
Both methods are compatible with batch normalization, which further stabilizes training. For a deeper dive into weight initialization techniques, explore this comprehensive guide.
Xavier/Glorot Initialization
Xavier initialization, also known as Glorot initialization, is a widely used technique in deep learning. It ensures that the variance of activations remains consistent across layers, promoting stable training. This method is particularly effective with activation functions like tanh and sigmoid.

How Xavier Initialization Works
The method derives its name from Xavier Glorot, who introduced it in 2010. It scales the initial weights based on the number of input and output neurons. The formula W[l] ~ N(0, 1/n[l-1]) ensures that the variance of activations is preserved during forward and backward propagation.
This approach prevents issues like vanishing or exploding gradients. By maintaining a balance, Xavier initialization allows signals to propagate effectively through the network. It’s especially useful in networks with tanh activations, where it helps achieve faster convergence.
When to Use Xavier Initialization
Xavier initialization is ideal for networks with moderate depth and activation functions like tanh or sigmoid. It’s less effective in very deep networks (over 50 layers) due to potential signal degradation. For ReLU-based networks, He initialization is often a better choice.
In Keras, developers can choose between GlorotUniform and GlorotNormal. Both methods aim to preserve variance, but they differ in their distribution types. GlorotNormal uses a normal distribution, while GlorotUniform relies on a uniform distribution.
- Effective for tanh and sigmoid activations.
- Preserves variance across layers.
- Less suitable for very deep networks.
- Available in Keras as GlorotUniform and GlorotNormal.
He Initialization for ReLU Activation
He initialization is a specialized technique designed to optimize training for models using ReLU activation. It addresses the unique challenges posed by ReLU’s zero gradient region, ensuring stable and efficient learning. This method scales parameters based on the number of input neurons, preserving variance across layers.
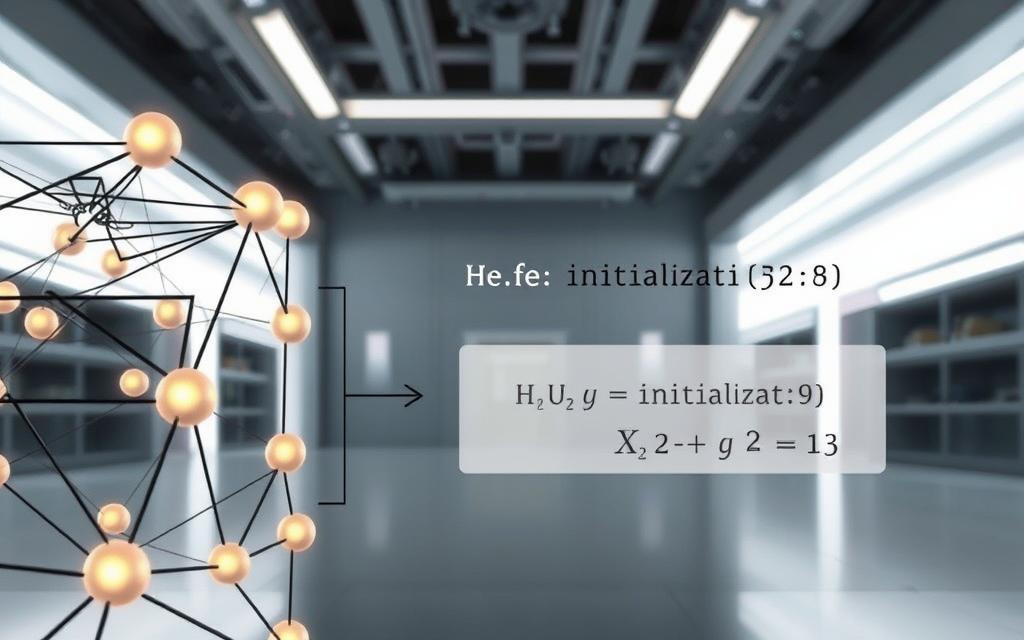
The formula W[l] ~ N(0, √(2/n[l-1])) ensures that signals propagate effectively during forward and backward propagation. This adjustment prevents issues like vanishing gradients, making it ideal for deep networks. Empirical studies on ImageNet classifiers have validated its effectiveness, especially in architectures with many layers.
He Uniform Initialization
He Uniform initialization samples values from a uniform distribution within a defined range. This approach is simple yet effective for breaking symmetry in early training stages. In Keras, it can be implemented as:
initializer = tf.keras.initializers.HeUniform()
This method is particularly useful in convolutional layers, where it helps maintain stable gradient flow.
He Normal Initialization
He Normal initialization draws values from a normal distribution with a mean of zero and a standard deviation of √(2/n[l-1]). This technique is widely used in networks with ReLU-based activations, including variants like leaky ReLU. Its Keras implementation is straightforward:
initializer = tf.keras.initializers.HeNormal()
Compared to Xavier initialization, He Normal performs better in deep residual networks, ensuring faster convergence and improved accuracy.
- Mathematical adjustment for ReLU’s zero gradient region.
- Empirical validation on ImageNet classifiers.
- Comparison with Xavier in deep residual networks.
- Implementation nuances in convolutional layers.
- Combined use with leaky ReLU variants.
Best Practices for Weight and Bias Initialization
Achieving optimal performance in deep learning models requires careful attention to parameter setup. Proper initialization ensures stable training and prevents issues like vanishing gradients or exploding gradients. By following best practices, developers can enhance model efficiency and accuracy.
Choosing the Right Initialization for Your Model
Selecting the appropriate method depends on your model’s architecture and activation function. For instance, Xavier initialization works well with tanh, while He initialization is ideal for ReLU. Consider the following factors:
- Network depth: Deeper networks may require specialized techniques like He initialization.
- Activation function: Match the initialization method to the function’s properties.
- Regularization: Combine initialization with techniques like gradient clipping for stability.
Common Pitfalls to Avoid
Improper setup can lead to training failures or poor model performance. Here are some common mistakes and how to address them:
| Pitfall | Solution |
|---|---|
| Vanishing gradients | Use Xavier or He initialization to maintain variance. |
| Exploding gradients | Apply gradient clipping or adjust learning rates. |
| Symmetry in neurons | Randomize initial values to break symmetry. |
Monitoring activation statistics during early training can help identify issues. Additionally, consider transfer learning initialization when adapting pre-trained models to new tasks. By following these best practices, you can ensure your model converges efficiently and delivers reliable results.
Conclusion
The success of deep learning models often hinges on initial configuration. Proper initialization ensures stable training and prevents issues like vanishing or exploding gradients. It directly impacts model accuracy and convergence speed.
Emerging trends, such as data-aware methods, are shaping the future of parameter setup. These techniques adapt to specific datasets, enhancing performance in complex architectures. Staying updated with these advancements is essential for practitioners.
For optimal results, choose methods like Xavier or He initialization based on your model’s activation function. Experimentation is key to finding the best approach for your specific use case. Resources like the Deep Learning Specialization offer valuable insights for further study.
Start implementing these strategies today to unlock the full potential of your machine learning models. Proper setup is the foundation of success in neural networks.
FAQ
Why is initialization important in neural networks?
Proper initialization ensures the model starts with values that allow efficient training. Poor initialization can lead to issues like vanishing or exploding gradients, hindering convergence.
What are the common challenges in weight initialization?
Challenges include setting values that prevent gradients from vanishing or exploding, ensuring symmetry breaking, and maintaining appropriate variance across layers.
How do weights and biases impact neural networks?
Weights determine the strength of connections between neurons, while biases allow the model to shift the activation function, enabling better fitting to data.
What is zero initialization, and why is it problematic?
Zero initialization sets all weights and biases to zero, which fails because it prevents neurons from learning independently, leading to identical updates during backpropagation.
What are the benefits of random initialization?
Random initialization breaks symmetry, allowing neurons to learn different features. It also helps avoid issues like vanishing gradients by starting with small, non-zero values.
How does Xavier initialization work?
Xavier initialization scales weights based on the number of input and output neurons, maintaining consistent variance across layers. It works well with sigmoid and tanh activation functions.
When should He initialization be used?
He initialization is ideal for models using ReLU activation functions. It adjusts the variance of weights to account for the non-linearity of ReLU, improving training stability.
What are the best practices for choosing an initialization method?
Select a method based on the activation function and network architecture. Avoid zero initialization, use Xavier for sigmoid/tanh, and He for ReLU. Experiment to find the best fit for your model.
What are common pitfalls to avoid during initialization?
Avoid setting all weights to zero, using inappropriate distributions, or ignoring the impact of activation functions. Always validate initialization choices with empirical testing.











